Exercise 7: Bayesian meta-analysis
In 2014, Crins et al. 1 published a meta-analysis assessing the incidence of acute rejection (AR) with or without Interleukin-2 receptor antagonists. In this exercise we will recreate this analysis.
Load the package
bayesmeta2 and the data from Crins et al. (2014) with theRcommanddata("CrinsEtAl2014").library(bayesmeta) data(CrinsEtAl2014)Play around with the companion shiny app at: https://rshiny.gwdg.de/apps/bayesmeta/.
If the website is unavailable, you can launch the app locally by running the 2 following commands from :library("shiny") install.packages("rhandsontable") runUrl("http://wwwuser.gwdg.de/~croever/bayesmeta/bayesmeta-app.zip")Directly in the console now, using the
escalc()function from the packagemetafor, compute the estimated log odds ratios from the 6 considered studies alongside their sampling variances (ProTip: read the Measures for Dichotomous Variables section from the help of theescalc()function). Check that those are the same as the one on the online shiny app (ProTip: ‘sigma’ is the standard error, i.e. the square root of the sampling variancevi)library("metafor") crins.es <- escalc(measure = "OR", ai = exp.AR.events, n1i = exp.total, ci = cont.AR.events, n2i = cont.total, slab = publication, data = CrinsEtAl2014) crins.es[, c("publication", "yi", "vi")]publication yi vi Heffron (2003) -2.3097026 0.3593718 Gibelli (2004) -0.4595323 0.3095760 Schuller (2005) -2.3025851 0.7750000 Ganschow (2005) -1.7578579 0.2078161 Spada (2006) -1.2584610 0.4121591 Gras (2008) -2.4178959 2.3372623 NB: Log-odds ratios are symmetric around zero and have a sampling distribution closer to the normal distibution than the natural OR scale. For this reason, they are usually prefered for meta-analyses. Their sample variance is then computed as the sum of the inverse of all the counts in the
Perform a random-effect meta-analysis of those data using the
bayesmeta()function from the packagebayesmeta, within . Use a uniform prior onres_crins_bayesmeta <- bayesmeta(y = crins.es$yi, sigma = sqrt(crins.es$vi), labels = crins.es$publication, tau.prior = function(t) { dunif(t, max = 4) }, mu.prior = c(0, 4), interval.type = "central") summary(res_crins_bayesmeta)## 'bayesmeta' object. ## data (6 estimates): ## y sigma ## Heffron (2003) -2.3097026 0.5994763 ## Gibelli (2004) -0.4595323 0.5563956 ## Schuller (2005) -2.3025851 0.8803408 ## Ganschow (2005) -1.7578579 0.4558685 ## Spada (2006) -1.2584610 0.6419962 ## Gras (2008) -2.4178959 1.5288107 ## ## tau prior (proper): ## function (t) ## { ## dunif(t, max = 4) ## } ## <bytecode: 0x11d2c90e8> ## ## mu prior (proper): ## normal(mean=0, sd=4) ## ## ML and MAP estimates: ## tau mu ## ML joint 0.3258895 -1.578317 ## ML marginal 0.4644136 -1.587347 ## MAP joint 0.3244300 -1.569497 ## MAP marginal 0.4644205 -1.576092 ## ## marginal posterior summary: ## tau mu theta ## mode 0.46442045 -1.5760916 -1.5656380 ## median 0.61810119 -1.5866193 -1.5806176 ## mean 0.73768542 -1.5935568 -1.5935568 ## sd 0.56879971 0.4698241 1.0448965 ## 95% lower 0.03724555 -2.5605641 -3.7989794 ## 95% upper 2.22766946 -0.6704235 0.5580817 ## ## (quoted intervals are central, equal-tailed credible intervals.) ## ## Bayes factors: ## tau=0 mu=0 ## actual 2.6800815 0.094852729 ## minimum 0.7442665 0.008342187 ## ## relative heterogeneity I^2 (posterior median): 0.4718317plot(res_crins_bayesmeta)
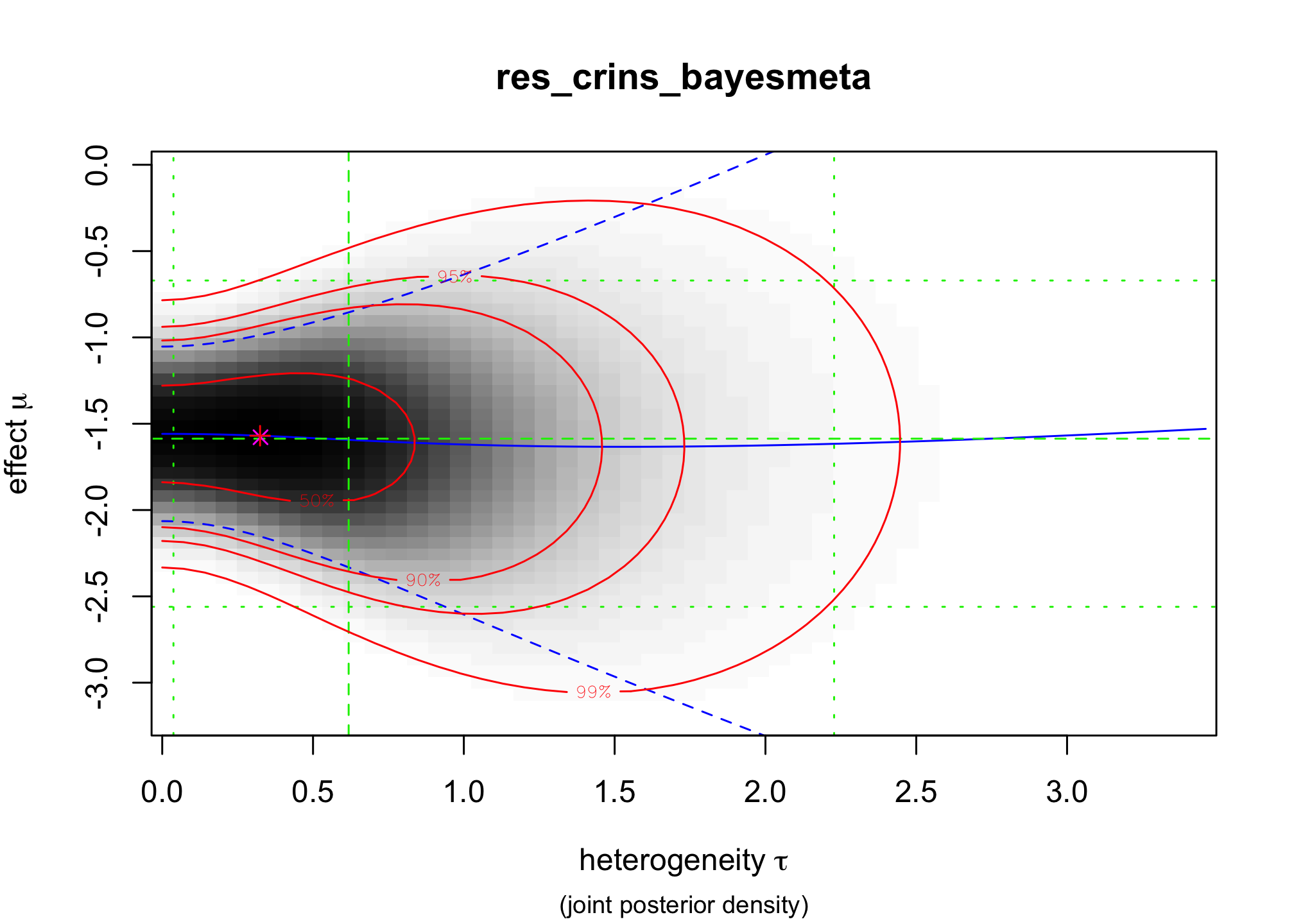
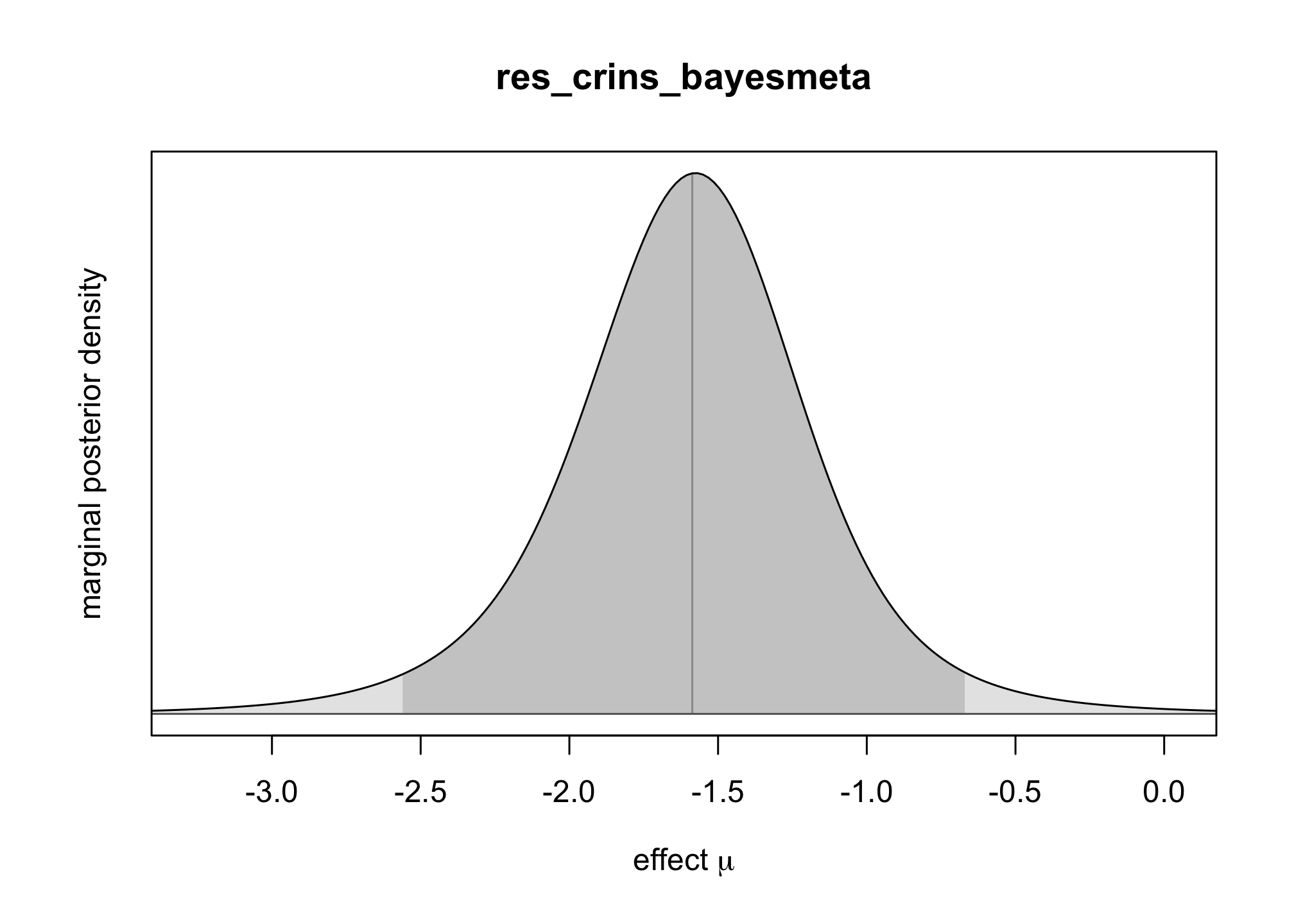
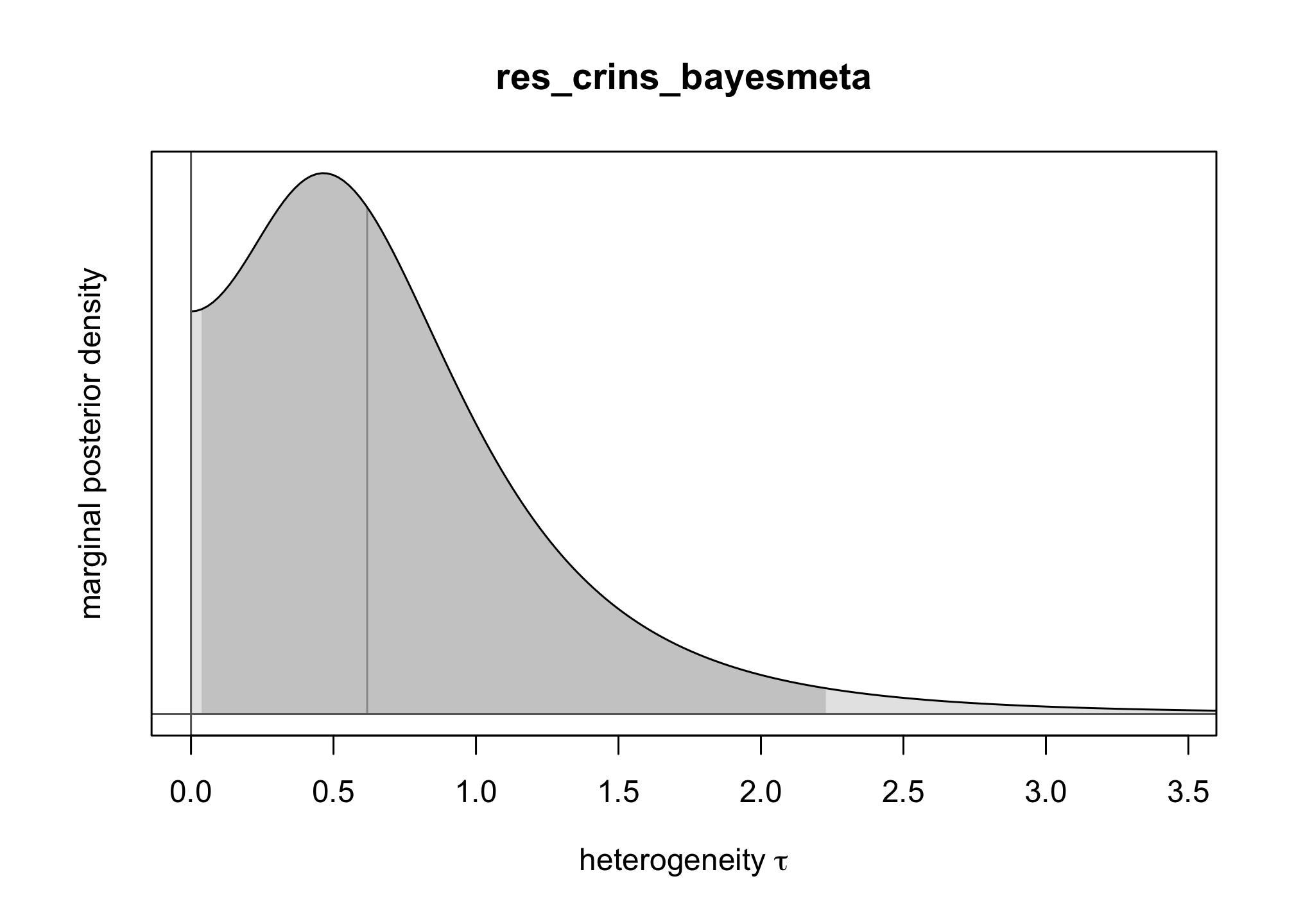
Write the corresponding random-effects Bayesian meta-analysis model (using words & math, not
BUGSand – yet).I) Question of interest:
Is the treatment (IL2RA) odds ratio for Acute Rejection events inferior to 1 ?
II) Sampling model:
LetUse
rjagsto estimate the same model, saving the BUGS model in a.txtfile (calledcrinsBUGSmodel.txtfor instance).# Random-effects model for Crins et al. 2014 Acute Rejection meta-analysis model{ # Sampling model/likelihood for (i in 1:N){ logOR[i]~dnorm(theta[i], precision.logOR[i]) theta[i]~dnorm(mu, precision.tau) } # Priors mu~dnorm(0, 0.0625) # 1/16 = 0.0625 tau~dunif(0, 4) # Re-parameterization for(i in 1:N){ precision.logOR[i] <- pow(sigma[i], -2) } precision.tau <- pow(tau, -2) OR <- exp(mu) }# Sampling library(rjags) crins_jags_res <- jags.model(file = "crinsBUGSmodel.txt", data = list(logOR = crins.es$yi, sigma = sqrt(crins.es$vi), N = length(crins.es$yi)), n.chains = 3)## Compiling model graph ## Resolving undeclared variables ## Allocating nodes ## Graph information: ## Observed stochastic nodes: 6 ## Unobserved stochastic nodes: 8 ## Total graph size: 34 ## ## Initializing modelres_crins_jags_res <- coda.samples(model = crins_jags_res, variable.names = c("mu", "tau"), n.iter = 20000) # Postprocessing res_crins_jags_res <- window(res_crins_jags_res, start = 5001) # remove burn-in for Markov chain convergence summary(res_crins_jags_res)## ## Iterations = 5001:21000 ## Thinning interval = 1 ## Number of chains = 3 ## Sample size per chain = 16000 ## ## 1. Empirical mean and standard deviation for each variable, ## plus standard error of the mean: ## ## Mean SD Naive SE Time-series SE ## mu -1.5904 0.4681 0.002137 0.00407 ## tau 0.7326 0.5674 0.002590 0.01109 ## ## 2. Quantiles for each variable: ## ## 2.5% 25% 50% 75% 97.5% ## mu -2.55827 -1.8481 -1.5880 -1.3228 -0.6639 ## tau 0.03584 0.3314 0.6125 0.9825 2.2137HDInterval::hdi(res_crins_jags_res)## mu tau ## lower -2.5388788 1.198287e-05 ## upper -0.6483598 1.819623e+00 ## attr(,"credMass") ## [1] 0.95plot(res_crins_jags_res)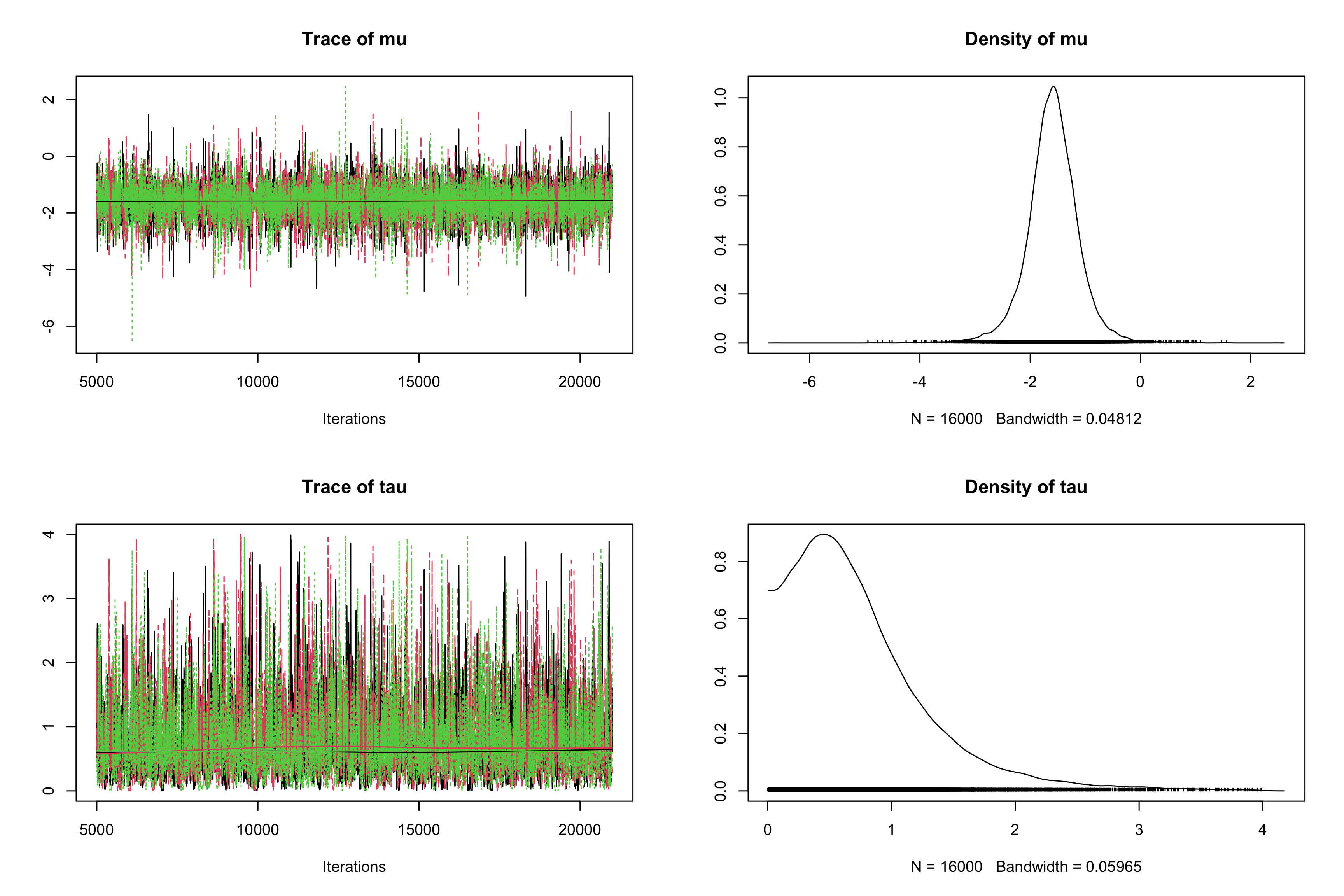
Nicola D Crins et al. “Interleukin-2 Receptor Antagonists for Pediatric Liver Transplant Recipients: A Systematic Review and Meta-Analysis of Controlled Studies,” Pediatric Transplantation 18, no. 8 (2014): 839–850, doi:10.1111/petr.12362.↩︎
Christian Röver “Bayesian Random-Effects Meta-Analysis Using the Bayesmeta R Package,” Journal of Statistical Software 93 (2020): 1–51, doi:10.18637/jss.v093.i06.↩︎
Joseph L. Fleiss and Jesse A. Berlin “Effect Sizes for Dichotomous Data,” in The Handbook of Research Synthesis and Meta-Analysis, 2nd Ed (New York, NY, US: Russell Sage Foundation, 2009), 237–253.↩︎