Exercise 8: Bayesian regression

We will now analyze data from the therapeutic clinical trial ALBI-ANRS 070 which compared the efficacy and tolerance of 3 anti-retroviral strategies among HIV-1 positive patients naive of any anti-retroviral treatment 1.

  1. Load the data from the albianrs_data.csv available here (ProTip: set stringsAsFactors = TRUE in read.delim())

    albi <- read.csv("albianrs_data.csv", stringsAsFactors = TRUE)
summary(albi)
    ##    PatientID     ViralLoad          CD4              CD4t       CD4sup500
##  ID112  :  7   Min.   :1.699   Min.   : 149.0   Min.   :3.494   No :558  
##  ID130  :  7   1st Qu.:2.042   1st Qu.: 377.0   1st Qu.:4.406   Yes:392  
##  ID139  :  7   Median :2.712   Median : 465.0   Median :4.644            
##  ID15   :  7   Mean   :2.907   Mean   : 491.8   Mean   :4.664            
##  ID156  :  7   3rd Qu.:3.692   3rd Qu.: 585.0   3rd Qu.:4.918            
##  ID163  :  7   Max.   :5.604   Max.   :1318.0   Max.   :6.025            
##  (Other):908                                                             
##    Treatment        Day             Visit      
##  AZT+3TC:315   Min.   :  0.00   Min.   :0.000  
##  d4t+ddI:322   1st Qu.: 29.00   1st Qu.:1.000  
##  switch :313   Median : 84.00   Median :3.000  
##                Mean   : 86.19   Mean   :2.946  
##                3rd Qu.:140.00   3rd Qu.:5.000  
##                Max.   :256.00   Max.   :6.000  
##

    The following variables are available:

  • PatientID : Patient ID
  • ViralLoad: Plasma viral load
  • CD4: CD4 T-cell lymphocites rate (in cell/mm3)
  • CD4t: transformed CD4 T-cell lymphocites rate (in cell/mm3) (CD4t = CD41/4)
  • CD4sup500: binary variable indicating wether CD4 cell counts is above 500
  • Treatment : Treatment group 1 (d4t + ddI), 2 (alternance) ou 3 (AZT + 3TC))
  • Day: Day of visit (since inclusion)
  • Visit: Visit number

Below is a quantitative summary of the characteristics of those variables.

Table 1: Summary of the Albi-ANRS-070 trial data
Variable N = 9501
ViralLoad 2.71 (2.04, 3.69)
CD4 465 (377, 585)
CD4t 4.64 (4.41, 4.92)
CD4sup500 392 (41%)
Treatment
    AZT+3TC 315 (33%)
    d4t+ddI 322 (34%)
    switch 313 (33%)
Day 84 (29, 140)
Visit
    0 146 (15%)
    1 140 (15%)
    2 136 (14%)
    3 130 (14%)
    4 128 (13%)
    5 135 (14%)
    6 135 (14%)
1 Median (IQR) or n (%)

NB: for simplicity, NA values have been omitted.

  1. First, we want to explain the CD4 rate (as a transformed variable) from the viral load

    1. Display CD4t in scatterplot as a function of the ViralLoad and color the points according to Treatment.

      library(ggplot2)
library(MetBrewer)
ggplot(albi, aes(y = CD4t, x = ViralLoad, color = Treatment)) + geom_point(alpha = 0.7) +
    MetBrewer::scale_color_met_d("Java") + theme_bw()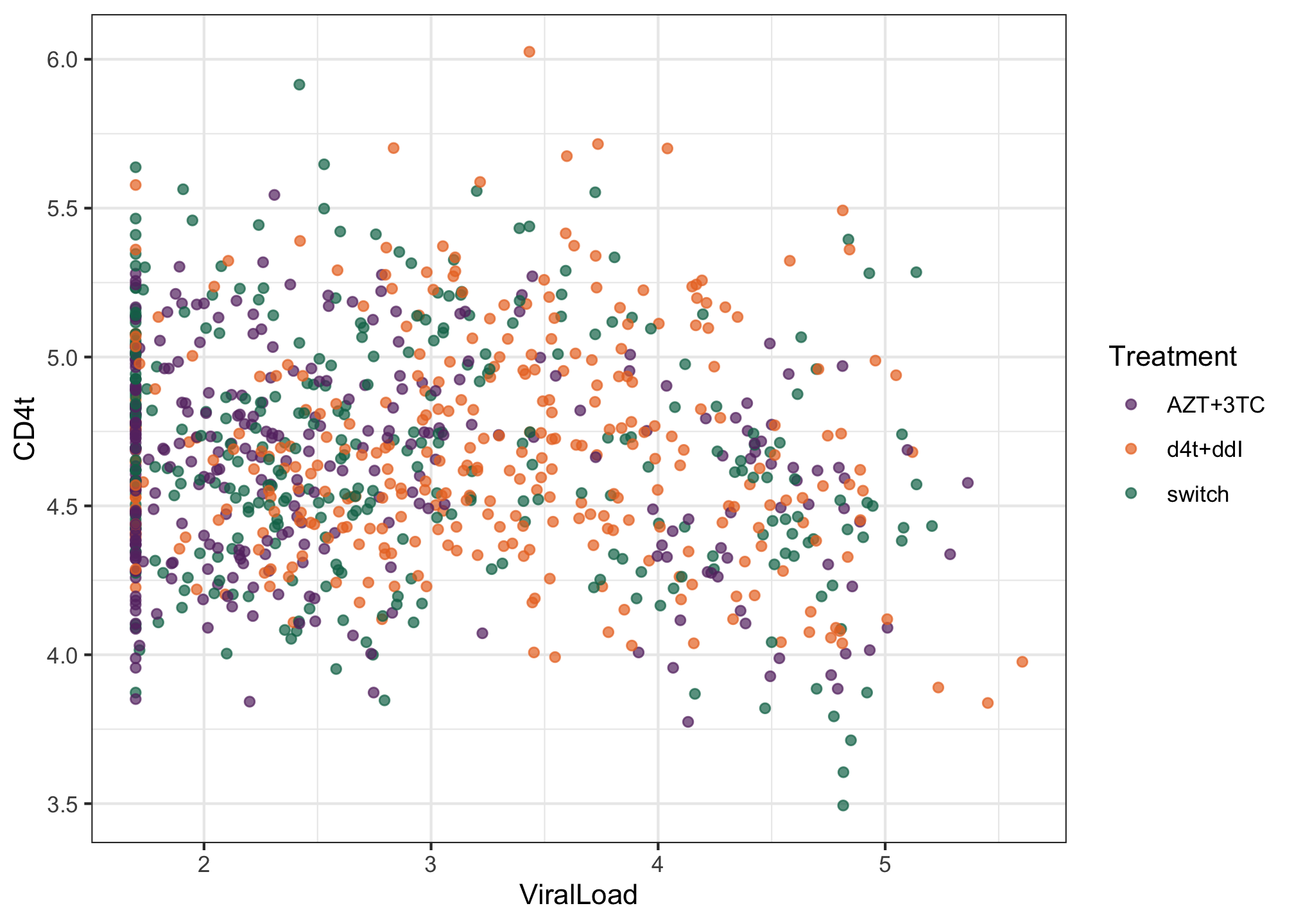

    2. Write down the Bayesian mathematical model corresponding to a linear regression of CD4t against the ViralLoad.

    I) Question of interest:
    How does the viral load linearly explains the (transformed) CD4 T-cell rate ?
    II) Sampling model:
    Let CD4ti be the ith (transformed) CD4 T-cell rate i and VLi2 the corresponding observed viral load: CD4ti∼iidN(β0+β1VLi,σ2) III) Priors: β0∼N(0,1002) β1∼N(0,1002) σ2∼InvGamma(0.001,0.001)


    1. Write the corresponding BUGS model and save it in an external .txt file.

      # Fixed effect linear regression Albi-ANRS
model{

  # Likelihood
  for (i in 1:N){ 
    CD4t[i]~dnorm(mu[i], tau)
    mu[i] <- beta0 + beta1*VL[i]
  }

  # Priors
  beta0~dnorm(0,0.0001) 
  beta1~dnorm(0,0.0001) # proper but very flat (vague: weakly informative)
  tau~dgamma(0.0001,0.0001) # proper but very flat (vague: weakly informative)

  # Parameters of interest
  sigma <- pow(tau, -0.5)
}

    2. Create the corresponding jags object in and generate a Monte Carlo sample of size 1000 for the 3 parameters of interest

      library(rjags)
albi_fixed_jags <- jags.model("albiBUGSmodel_fixed.txt", data = list(CD4t = albi$CD4t,
    N = nrow(albi), VL = albi$ViralLoad), n.chains = 3)
      ## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 950
##    Unobserved stochastic nodes: 3
##    Total graph size: 3195
## 
## Initializing model
      res_albi_fixed <- coda.samples(model = albi_fixed_jags, variable.names = c("beta0",
    "beta1", "sigma"), n.iter = 1000)

    3. Before interpreting the results, check the convergence. What do you notice ?

      library(coda)
plot(res_albi_fixed)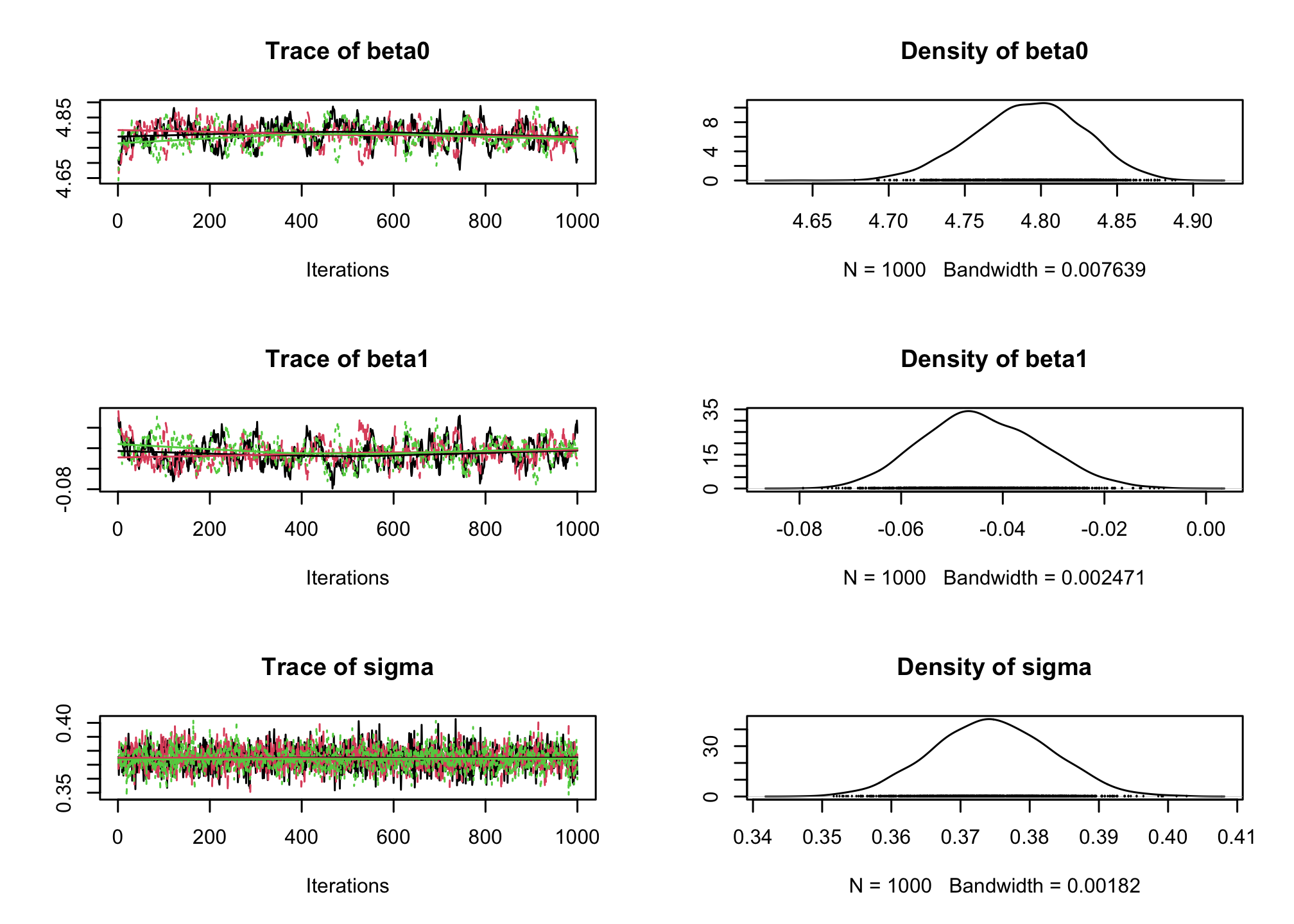

      gelman.plot(res_albi_fixed)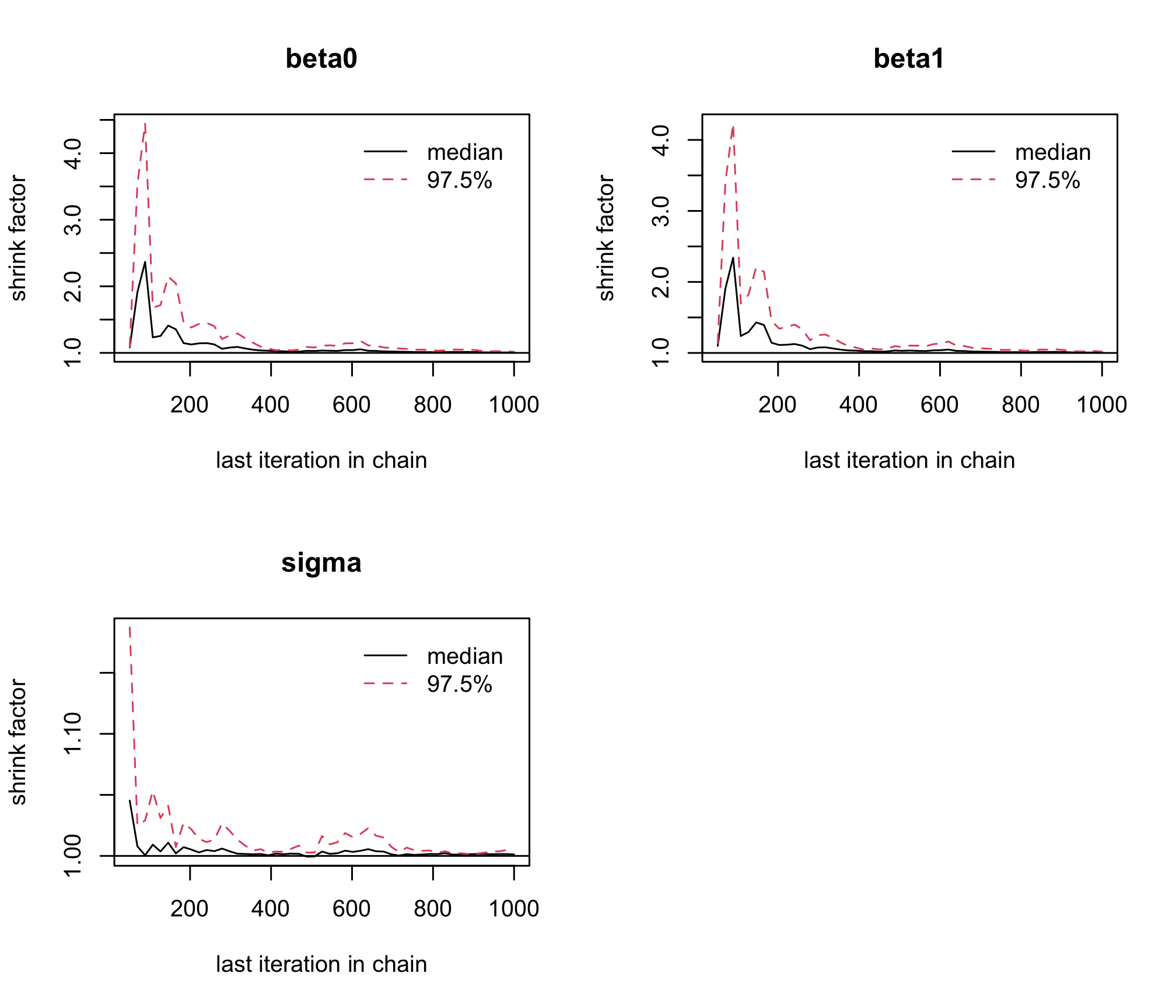

      acfplot(res_albi_fixed)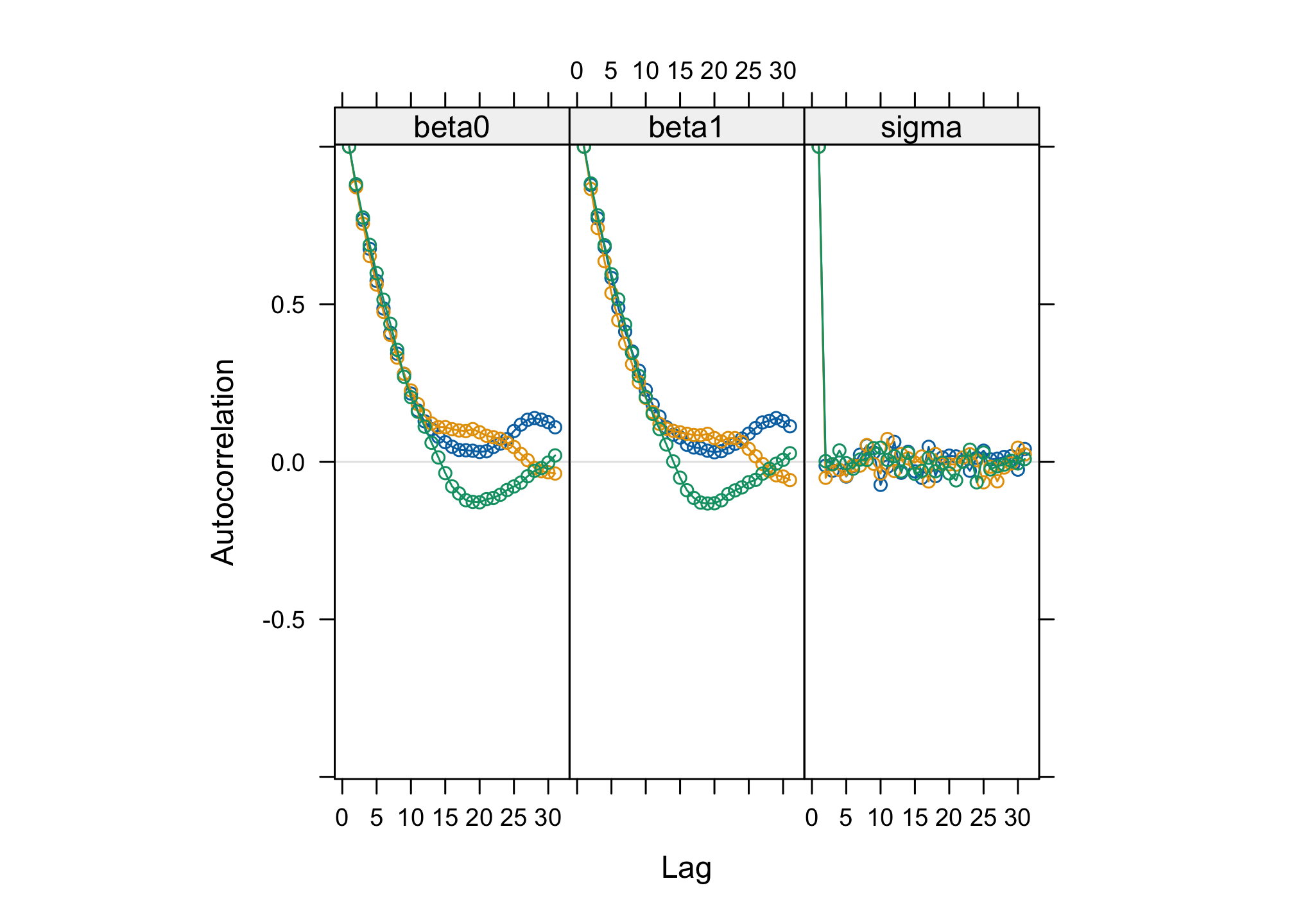

      par(mfrow = c(3, 3))
cumuplot(res_albi_fixed, ask = FALSE, auto.layout = FALSE)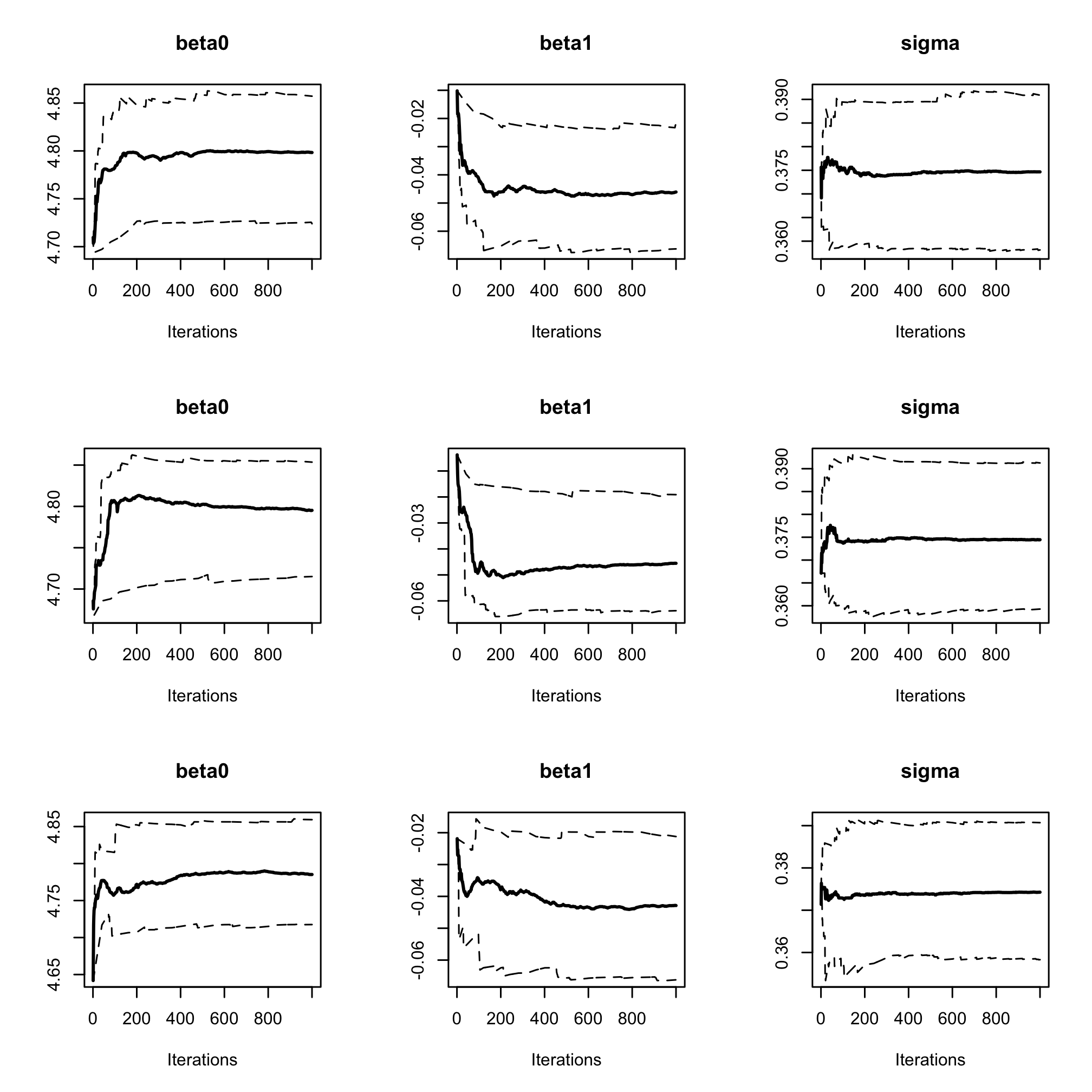

    4. Using the window function, remove the 500 first iterations as burn-in to reach Markov Chain convergence to its stationary distribution (the posterior). Is it sufficient to solve convergence issues ?

      res_albi_fixed2 <- window(res_albi_fixed, start = 501)

gelman.plot(res_albi_fixed2)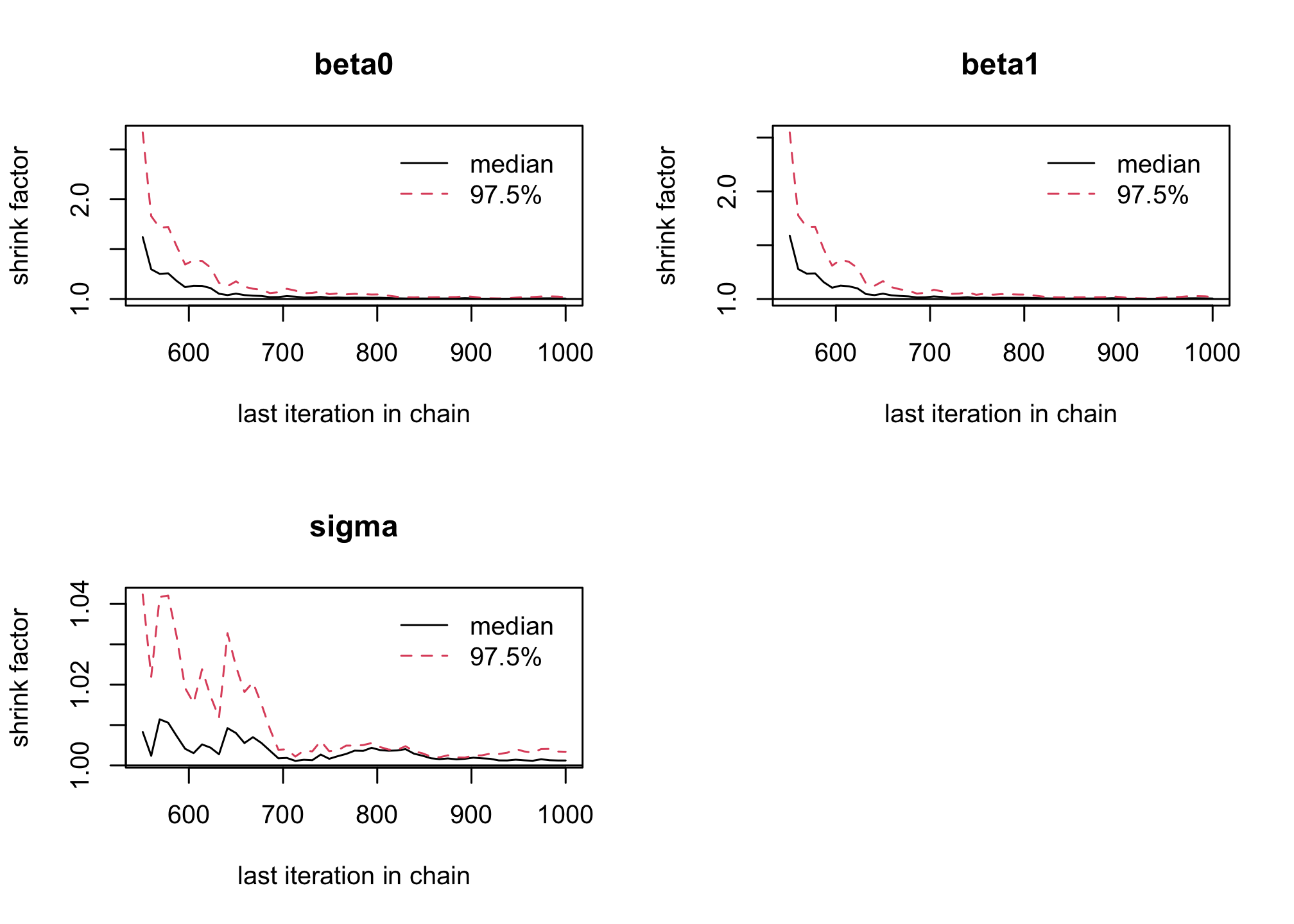

      acfplot(res_albi_fixed2)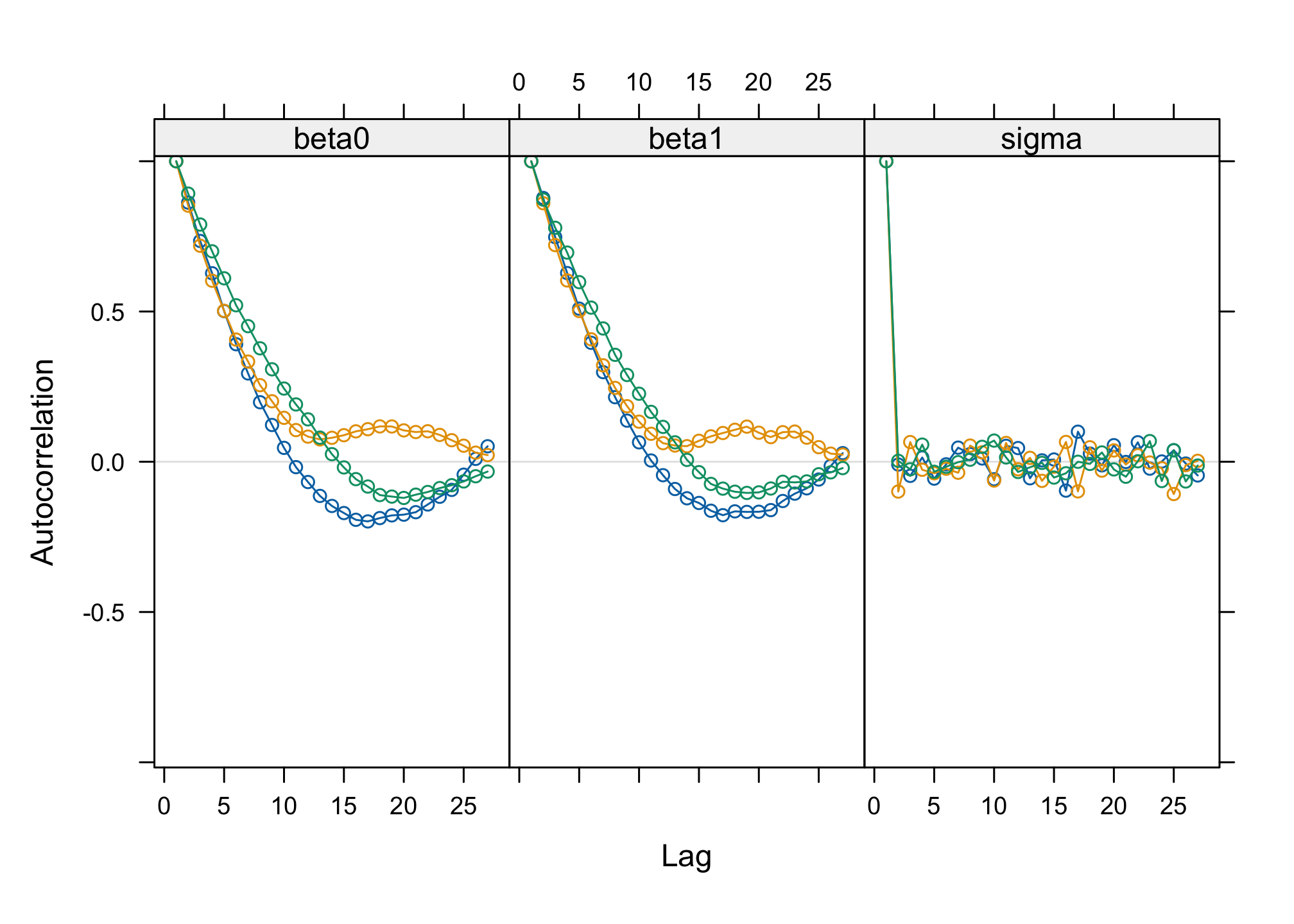

    5. Check the effective sample size of the Monte Carlo sample with the effectiveSize() function. Reduce auto-correlation by increasing the thin parameter to 10 in coda.samples. Check the impact on the effective sample

      `?`(effectiveSize)
effectiveSize(res_albi_fixed2)
      ##     beta0     beta1     sigma 
##  119.0255  117.9688 1608.7182
      albi_fixed_jags <- jags.model("albiBUGSmodel_fixed.txt", data = list(CD4t = albi$CD4t,
    N = nrow(albi), VL = albi$ViralLoad), n.chains = 3)
      ## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 950
##    Unobserved stochastic nodes: 3
##    Total graph size: 3195
## 
## Initializing model
      res_albi_fixed_thin <- coda.samples(model = albi_fixed_jags, variable.names = c("beta0",
    "beta1", "sigma"), n.iter = 10000, thin = 10)
res_albi_fixed_thin <- window(res_albi_fixed_thin, start = 5001)

effectiveSize(res_albi_fixed_thin)
      ##     beta0     beta1     sigma 
##  697.3918  645.3890 1567.0829
      plot(res_albi_fixed_thin)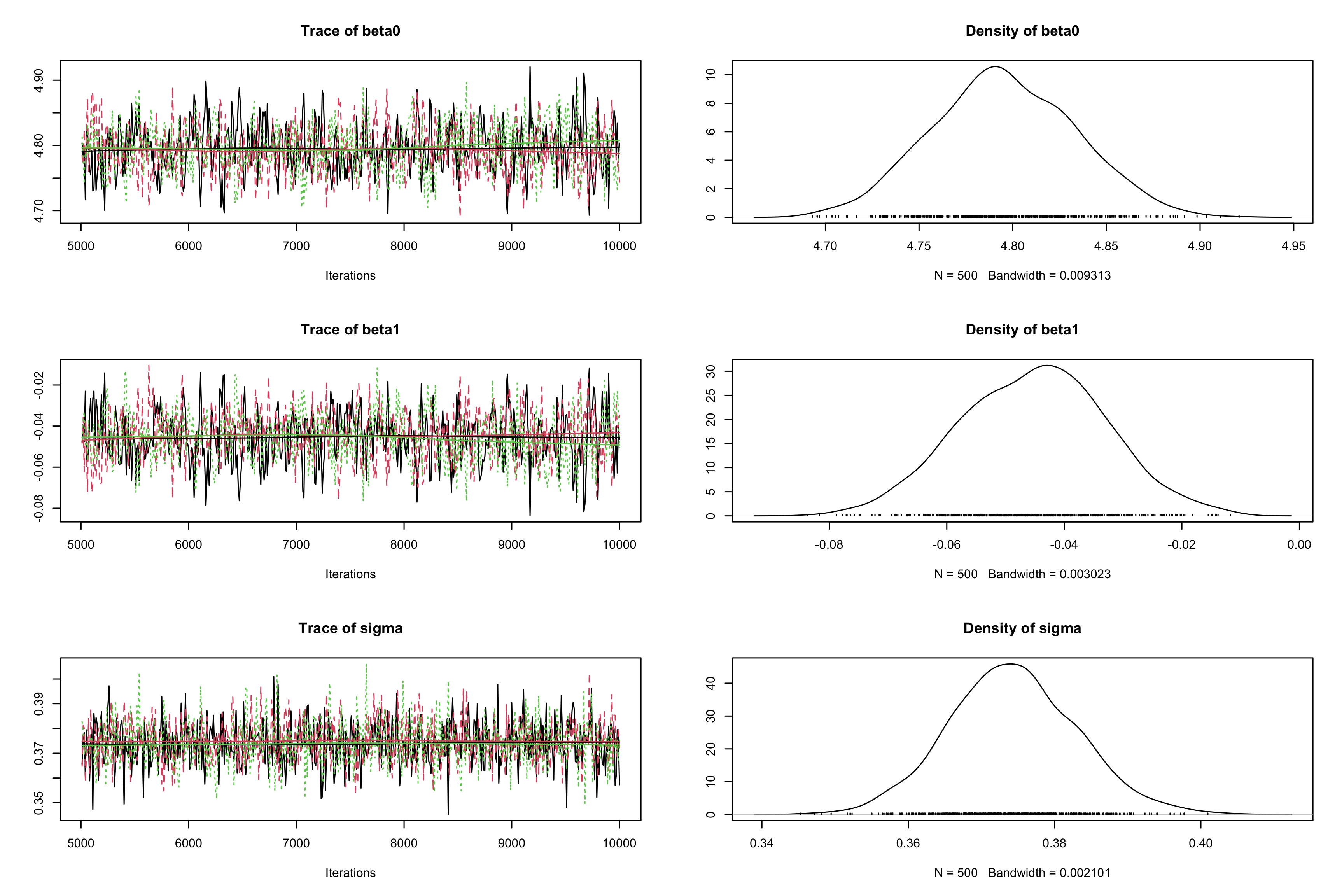

      gelman.plot(res_albi_fixed_thin)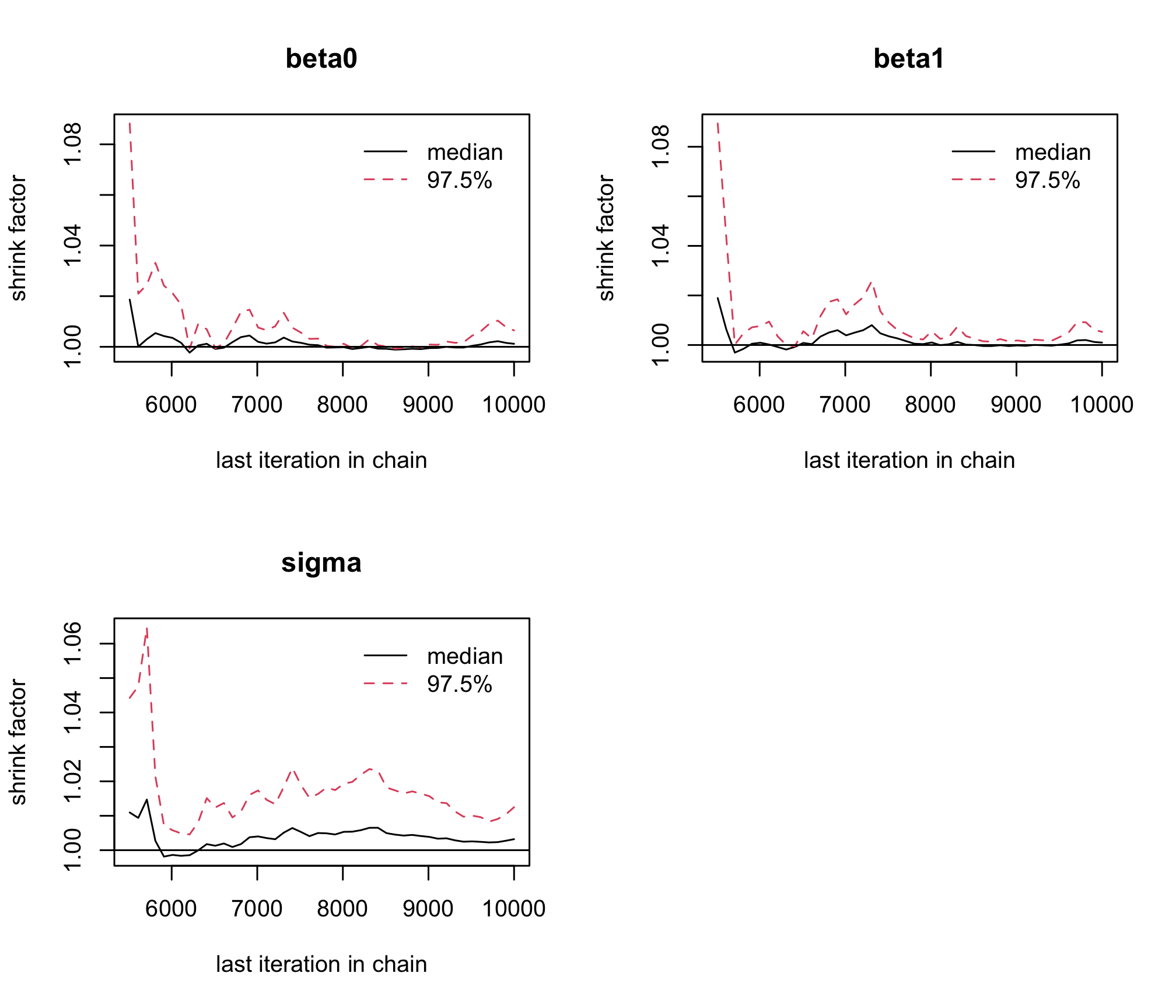

      acfplot(res_albi_fixed_thin)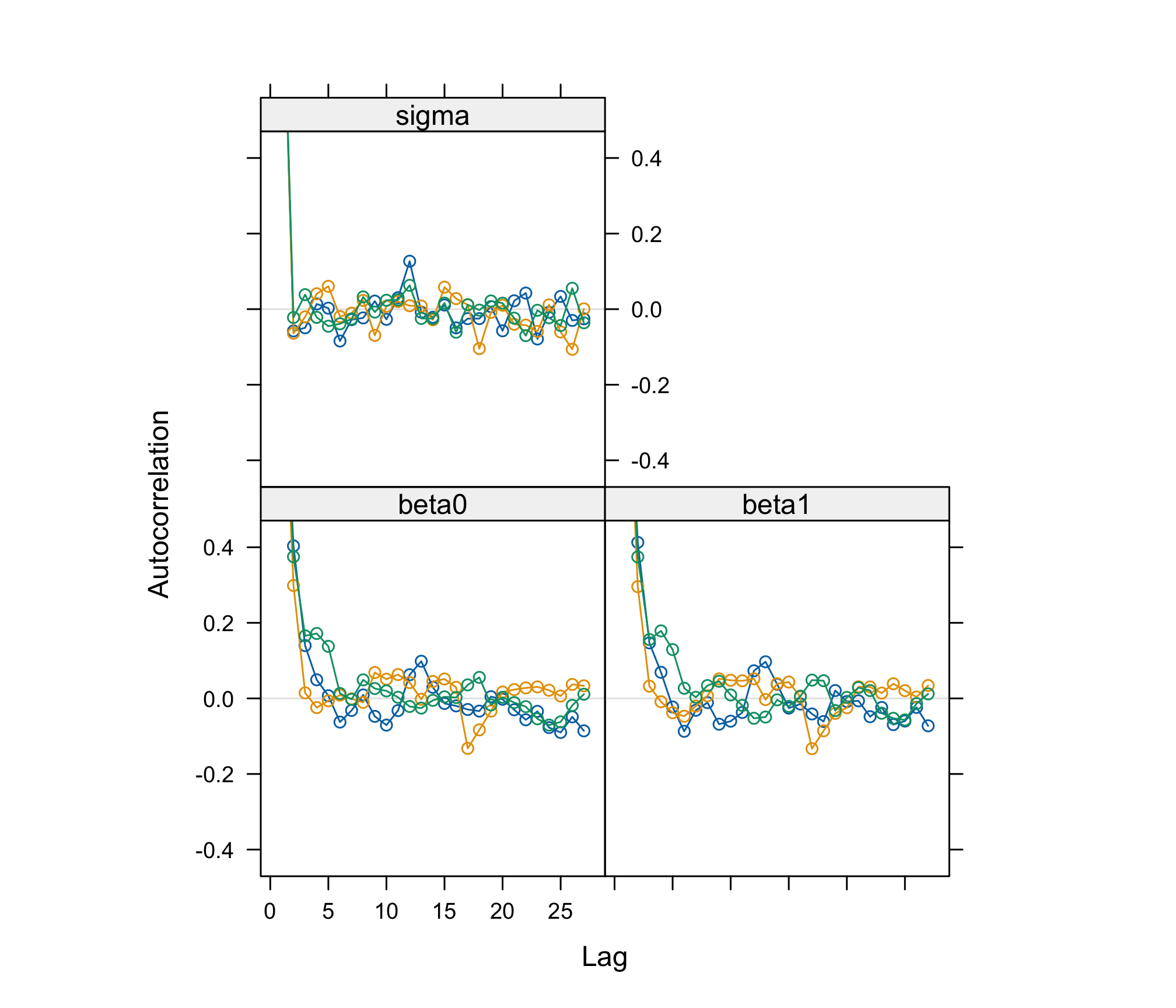

      par(mfrow = c(3, 3))
cumuplot(res_albi_fixed_thin, ask = FALSE, auto.layout = FALSE)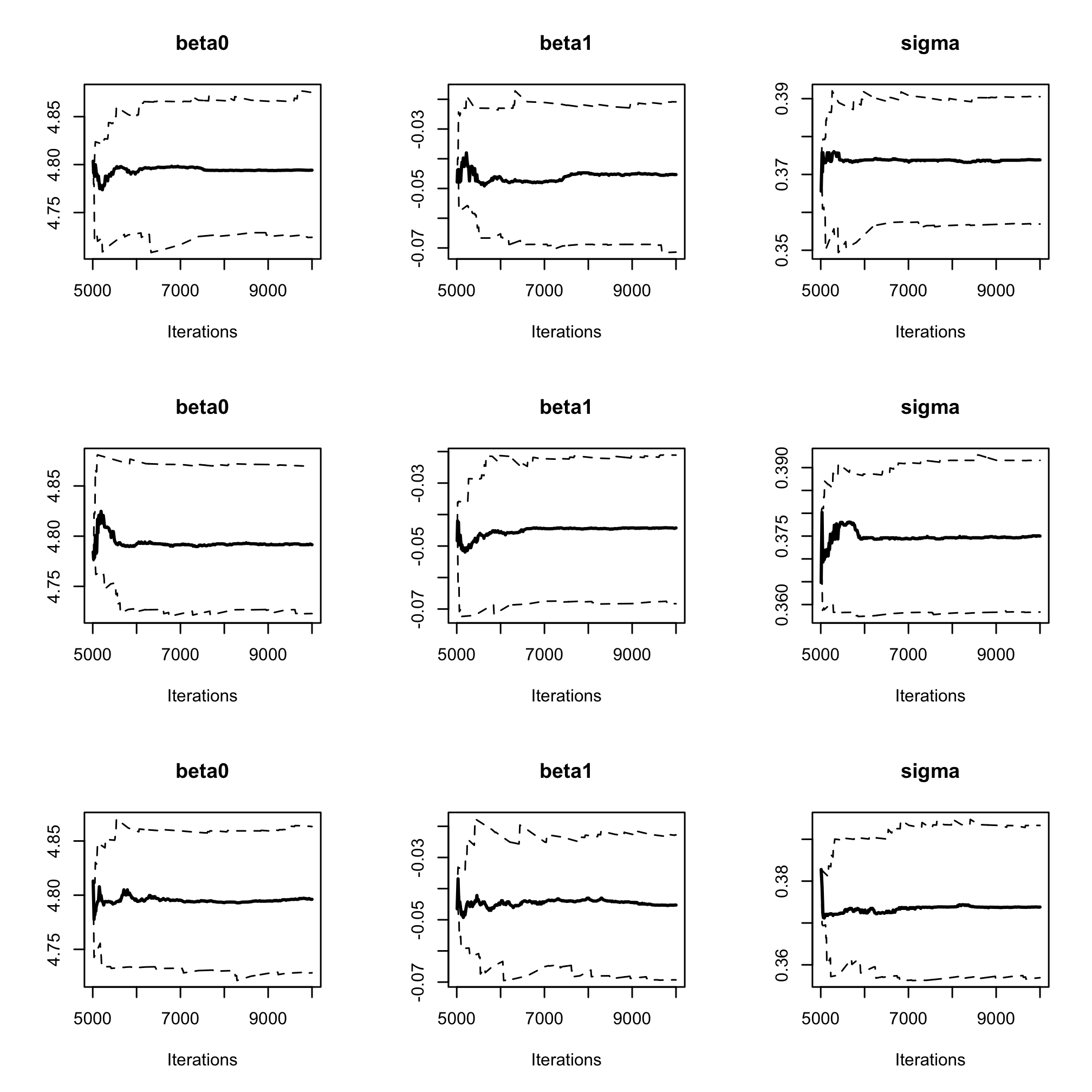

      summary(res_albi_fixed_thin)
      ## 
## Iterations = 5010:10000
## Thinning interval = 10 
## Number of chains = 3 
## Sample size per chain = 500 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##           Mean       SD  Naive SE Time-series SE
## beta0  4.79520 0.037932 0.0009794      0.0014860
## beta1 -0.04529 0.012314 0.0003179      0.0004939
## sigma  0.37429 0.008766 0.0002263      0.0002219
## 
## 2. Quantiles for each variable:
## 
##           2.5%      25%      50%      75%    97.5%
## beta0  4.72417  4.76969  4.79415  4.82216  4.86880
## beta1 -0.06898 -0.05388 -0.04489 -0.03683 -0.02111
## sigma  0.35744  0.36842  0.37413  0.37989  0.39242

  2. Compare those results with a frequentist analysis.

    freq_mod <- lm(CD4t ~ ViralLoad, data = albi)
summary(freq_mod)
    ## 
## Call:
## lm(formula = CD4t ~ ViralLoad, data = albi)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0828 -0.2604 -0.0197  0.2449  1.3856 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.79635    0.03696   129.8  < 2e-16 ***
## ViralLoad   -0.04564    0.01201    -3.8 0.000154 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3742 on 948 degrees of freedom
## Multiple R-squared:  0.01501,	Adjusted R-squared:  0.01397 
## F-statistic: 14.44 on 1 and 948 DF,  p-value: 0.0001537
    confint(freq_mod)
    ##                   2.5 %      97.5 %
## (Intercept)  4.72381166  4.86888881
## ViralLoad   -0.06921147 -0.02207249

  3. Perform a Bayesian logistic regression to study the impact of the treatment on the binary outcome CD4sup500 adjusted on the viral load. Once you have a first estimation, try adding an interaction between the treatment and the viral load.

    # Fixed effect logistic regression Albi-ANRS
model{

  # likelihood
  for (i in 1:N){
    CD4sup500[i] ~ dbern(proba[i])
    logit(proba[i]) <- beta0 + beta1*VL[i] + beta2*Tt_switch[i] + beta3*d4t[i] + beta4*VL[i]*d4t[i] +         beta5*VL[i]*Tt_switch[i]
  }

  #Priors
  beta0~dnorm(0,0.0001)
  beta1~dnorm(0,0.0001)
  beta2~dnorm(0,0.0001)
  beta3~dnorm(0,0.0001)
  beta4~dnorm(0,0.0001)
  beta5~dnorm(0,0.0001)

  #ORs
  OR_VL <- exp(beta1)
  OR_switch <- exp(beta2)
  OR_d4t <- exp(beta3)
  OR_d4tVL <- exp(beta4)
  OR_swVL <- exp(beta5)
}
    library(rjags)
albi_logis_jags <- jags.model("albiBUGSmodel_logistic_fixed.txt", data = list(CD4sup500 = 1 *
    (albi$CD4sup500 == "Yes"), N = nrow(albi), VL = albi$ViralLoad, d4t = 1 * (albi$Treatment ==
    "d4t+ddI"), Tt_switch = 1 * (albi$Treatment == "switch")), n.chains = 3)
    ## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 950
##    Unobserved stochastic nodes: 6
##    Total graph size: 7299
## 
## Initializing model
    res_albi_logis <- coda.samples(model = albi_logis_jags, variable.names = c("OR_VL",
    "OR_switch", "OR_d4t", "OR_d4tVL", "OR_swVL"), n.iter = 10000)
res_albi_logis_burnt <- window(res_albi_logis, start = 5001)

plot(res_albi_logis_burnt)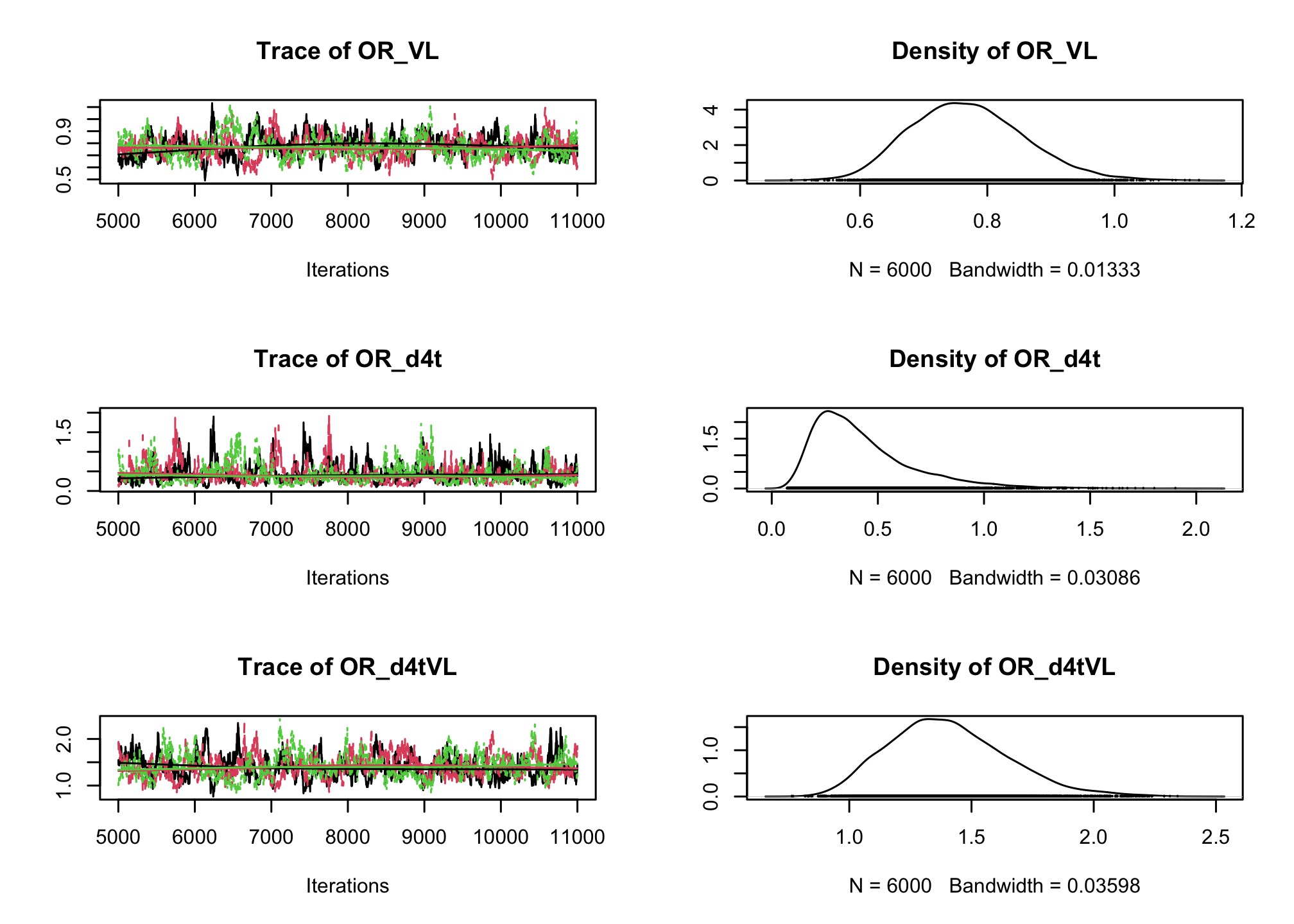

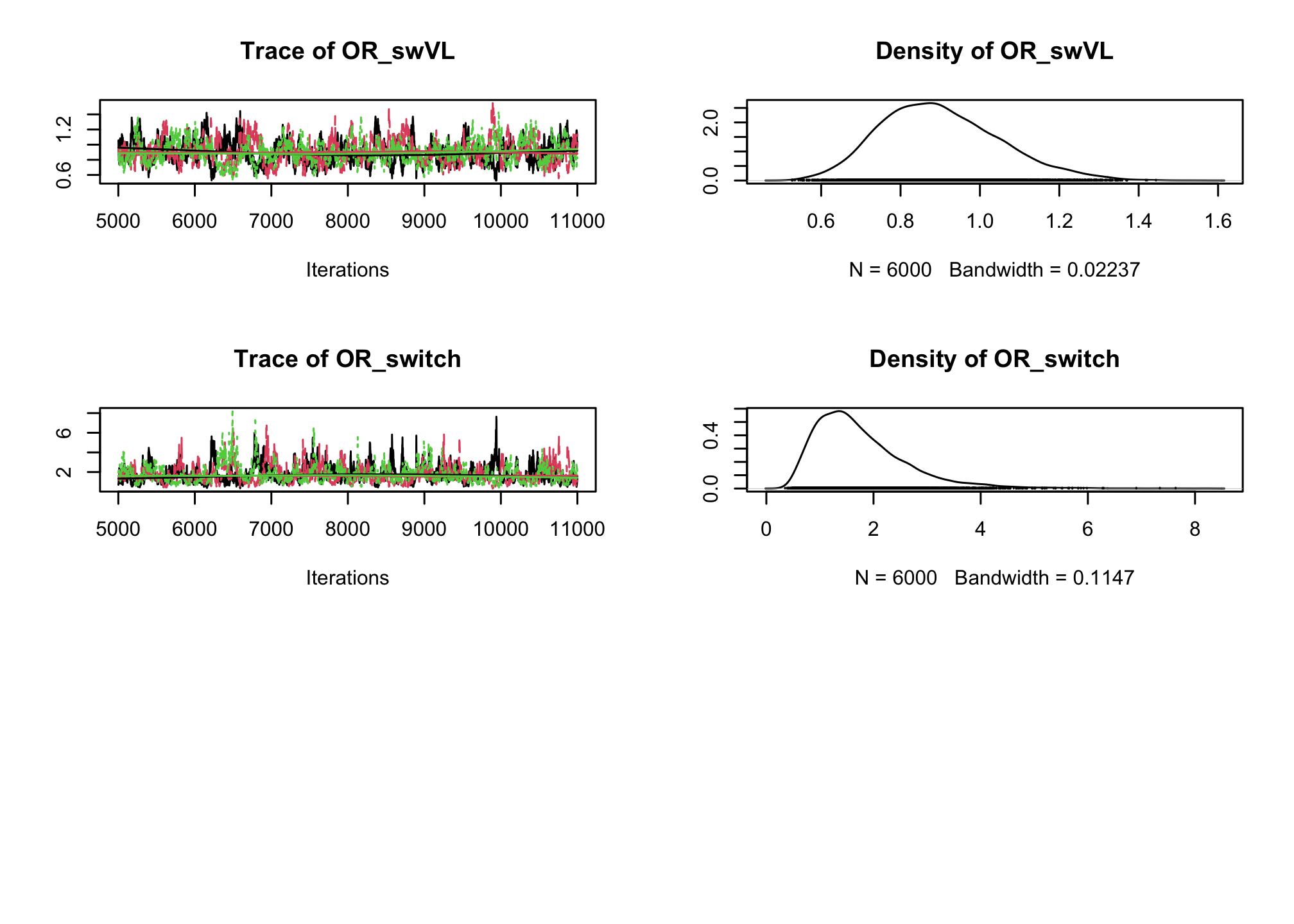
    summary(res_albi_logis_burnt)
    ## 
## Iterations = 5001:11000
## Thinning interval = 1 
## Number of chains = 3 
## Sample size per chain = 6000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##             Mean      SD  Naive SE Time-series SE
## OR_VL     0.7700 0.08925 0.0006653       0.006531
## OR_d4t    0.4285 0.23862 0.0017785       0.016362
## OR_d4tVL  1.4041 0.24089 0.0017955       0.016002
## OR_swVL   0.9012 0.14977 0.0011163       0.008414
## OR_switch 1.7516 0.86748 0.0064659       0.048294
## 
## 2. Quantiles for each variable:
## 
##             2.5%    25%    50%    75%  97.5%
## OR_VL     0.6134 0.7067 0.7654 0.8275 0.9595
## OR_d4t    0.1362 0.2576 0.3688 0.5344 1.0461
## OR_d4tVL  0.9967 1.2323 1.3850 1.5552 1.9364
## OR_swVL   0.6442 0.7924 0.8876 0.9970 1.2291
## OR_switch 0.6214 1.1350 1.5697 2.1640 3.9656
    summary(glm(CD4sup500 == "Yes" ~ ViralLoad * Treatment, family = "binomial", data = albi))
    ## 
## Call:
## glm(formula = CD4sup500 == "Yes" ~ ViralLoad * Treatment, family = "binomial", 
##     data = albi)
## 
## Coefficients:
##                            Estimate Std. Error z value Pr(>|z|)  
## (Intercept)                  0.3279     0.3241   1.012   0.3117  
## ViralLoad                   -0.2556     0.1197  -2.135   0.0328 *
## Treatmentd4t+ddI            -0.9409     0.5338  -1.763   0.0779 .
## Treatmentswitch              0.4836     0.4807   1.006   0.3143  
## ViralLoad:Treatmentd4t+ddI   0.3084     0.1737   1.776   0.0757 .
## ViralLoad:Treatmentswitch   -0.1303     0.1690  -0.771   0.4409  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 1287.8  on 949  degrees of freedom
## Residual deviance: 1270.9  on 944  degrees of freedom
## AIC: 1282.9
## 
## Number of Fisher Scoring iterations: 4

  4. So far we have ignored the longitudinal nature of our measurements. Now, lets add a random intercept in our logistic regression to account for the intra-patient correlation across visits.

    ggplot(albi, aes(y = CD4, x = Day, color = Treatment)) + geom_hline(aes(yintercept = 500),
    color = "grey35", linetype = 2) + geom_line(aes(group = PatientID), alpha = 0.3) +
    MetBrewer::scale_color_met_d("Java") + theme_bw()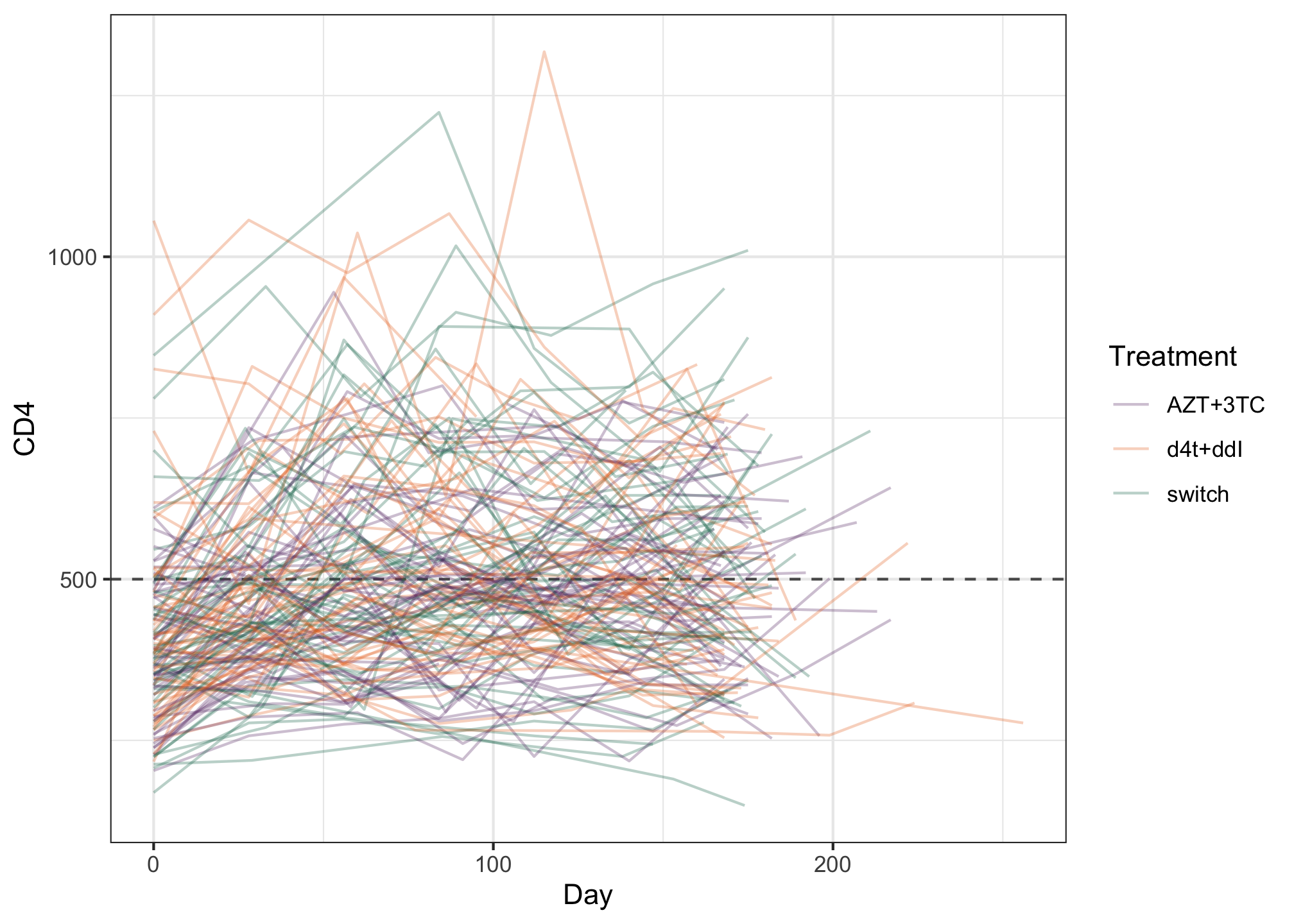

      # Mixed effect logistic regression Albi-ANRS
  model{

    # likelihood
    for (i in 1:N){
      CD4sup500[i] ~ dbern(proba[i])
      logit(proba[i]) <- beta0 + b0[PAT_ID[i]] + beta1*VL[i] + beta2*Tt_switch[i] + beta3*d4t[i] + beta4*VL[i]*d4t[i] +         beta5*VL[i]*Tt_switch[i]
    }

    for (j in 1:Npat){
      b0[j]~dnorm(0, tau_b0)
    }

    #Priors
    beta0~dnorm(0,0.0001)
    beta1~dnorm(0,0.0001)
    beta2~dnorm(0,0.0001)
    beta3~dnorm(0,0.0001)
    beta4~dnorm(0,0.0001)
    beta5~dnorm(0,0.0001)
    tau_b0~dgamma(0.001,0.001)

    #ORs
    OR_VL <- exp(beta1)
    OR_switch <- exp(beta2)
    OR_d4t <- exp(beta3)
    OR_d4tVL <- exp(beta4)
    OR_swVL <- exp(beta5)
    sigma_RI <- pow(tau_b0, -0.5)
  }
    library(rjags)
albi_logis_RI_jags <- jags.model("albiBUGSmodel_logistic_RandomInt.txt", data = list(CD4sup500 = 1 *
    (albi$CD4sup500 == "Yes"), N = nrow(albi), VL = albi$ViralLoad, d4t = 1 * (albi$Treatment ==
    "d4t+ddI"), Tt_switch = 1 * (albi$Treatment == "switch"), Npat = length(levels(albi$PatientID)),
    PAT_ID = as.numeric(albi$PatientID)), n.chains = 3)
    ## Compiling model graph
##    Resolving undeclared variables
##    Allocating nodes
## Graph information:
##    Observed stochastic nodes: 950
##    Unobserved stochastic nodes: 156
##    Total graph size: 8670
## 
## Initializing model
    res_albi_logis_RI <- coda.samples(model = albi_logis_RI_jags, variable.names = c("OR_VL",
    "OR_switch", "OR_d4t", "OR_d4tVL", "OR_swVL", "sigma_RI"), n.iter = 10000)
res_albi_logis_RI_burnt <- window(res_albi_logis_RI, start = 1001)

plot(res_albi_logis_RI_burnt)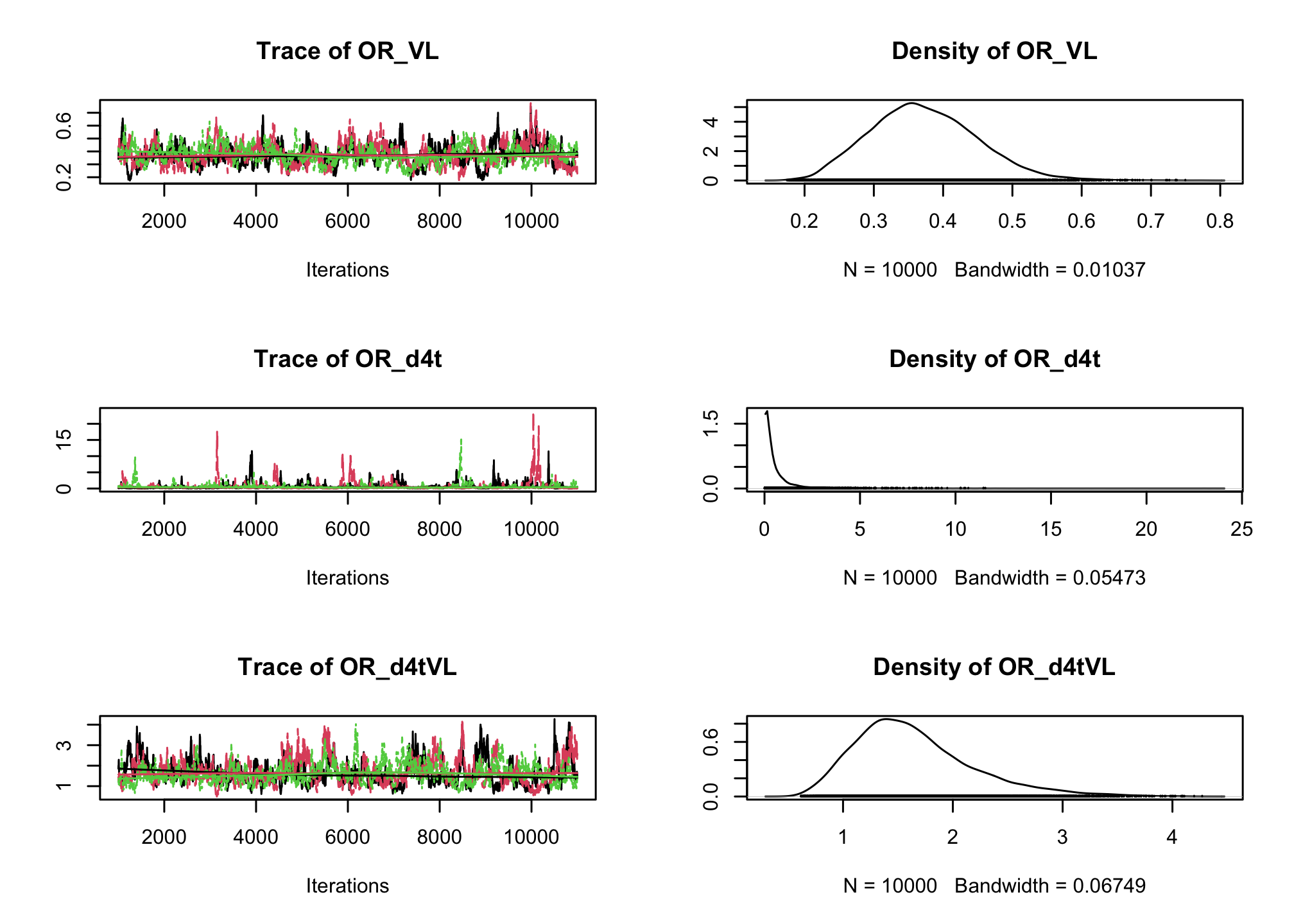

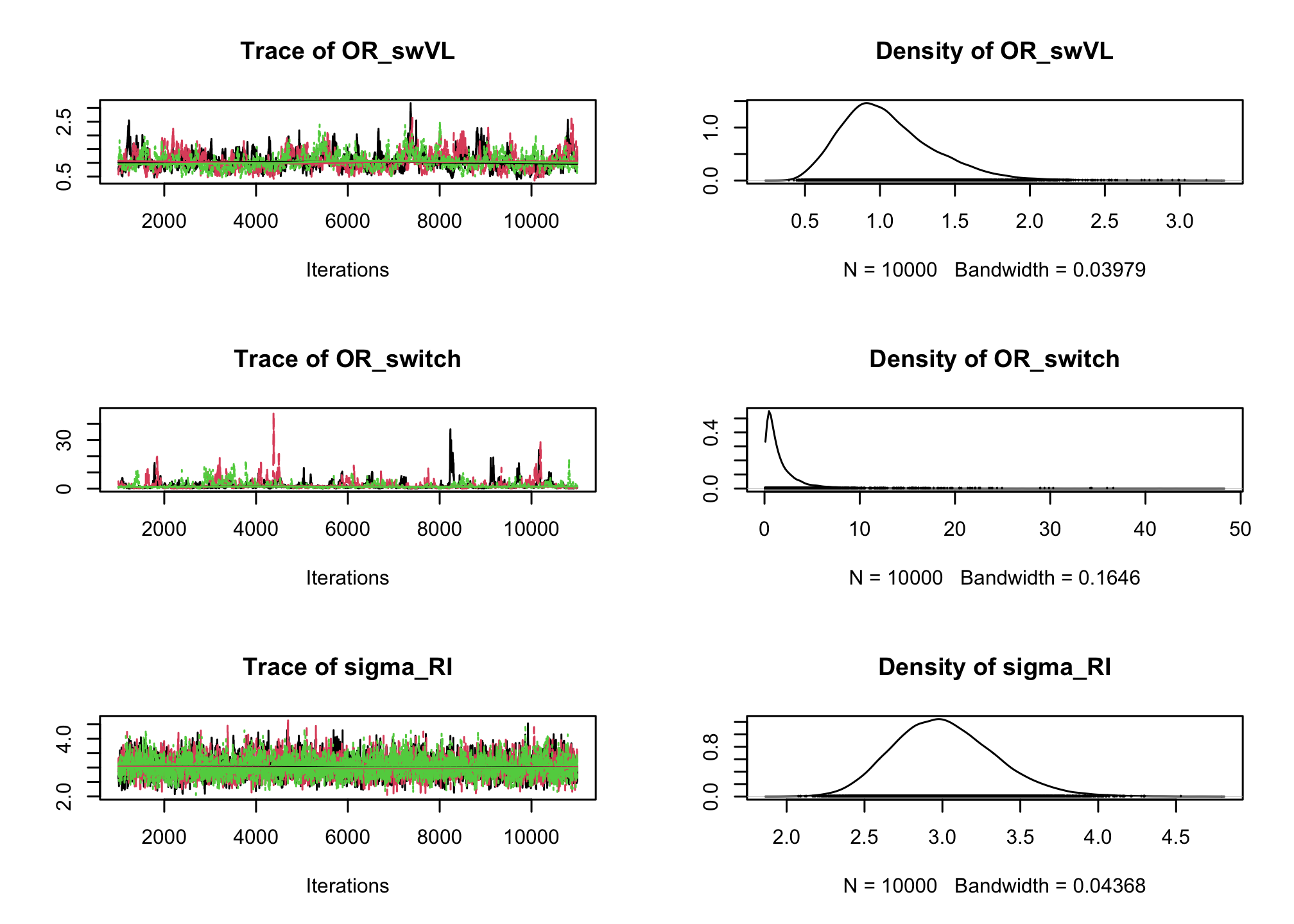
    summary(res_albi_logis_RI_burnt)
    ## 
## Iterations = 1001:11000
## Thinning interval = 1 
## Number of chains = 3 
## Sample size per chain = 10000 
## 
## 1. Empirical mean and standard deviation for each variable,
##    plus standard error of the mean:
## 
##             Mean      SD Naive SE Time-series SE
## OR_VL     0.3725 0.07691 0.000444       0.004670
## OR_d4t    0.6352 1.13532 0.006555       0.061109
## OR_d4tVL  1.6485 0.54363 0.003139       0.034870
## OR_swVL   1.0544 0.31312 0.001808       0.017495
## OR_switch 1.8321 2.41479 0.013942       0.122489
## sigma_RI  3.0162 0.32610 0.001883       0.006224
## 
## 2. Quantiles for each variable:
## 
##             2.5%    25%    50%    75%  97.5%
## OR_VL     0.2366 0.3183 0.3677 0.4221 0.5325
## OR_d4t    0.0321 0.1370 0.3070 0.6808 3.3165
## OR_d4tVL  0.8316 1.2657 1.5620 1.9363 2.9791
## OR_swVL   0.5749 0.8327 1.0062 1.2281 1.7807
## OR_switch 0.1492 0.5436 1.0792 2.1791 8.1893
## sigma_RI  2.4420 2.7881 2.9946 3.2221 3.7113
    library(lme4)
summary(lme4::glmer(CD4sup500 == "Yes" ~ (1 | PatientID) + ViralLoad * Treatment,
    family = "binomial", data = albi))
    ## Generalized linear mixed model fit by maximum likelihood (Laplace
##   Approximation) [glmerMod]
##  Family: binomial  ( logit )
## Formula: CD4sup500 == "Yes" ~ (1 | PatientID) + ViralLoad * Treatment
##    Data: albi
## 
##       AIC       BIC    logLik -2*log(L)  df.resid 
##     971.8    1005.8    -478.9     957.8       943 
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -2.9273 -0.4021 -0.1947  0.4119  3.9688 
## 
## Random effects:
##  Groups    Name        Variance Std.Dev.
##  PatientID (Intercept) 7.317    2.705   
## Number of obs: 950, groups:  PatientID, 149
## 
## Fixed effects:
##                             Estimate Std. Error z value Pr(>|z|)    
## (Intercept)                 1.901075   0.689952   2.755  0.00586 ** 
## ViralLoad                  -0.955590   0.212725  -4.492 7.05e-06 ***
## Treatmentd4t+ddI           -1.177377   1.103323  -1.067  0.28592    
## Treatmentswitch             0.101717   1.000232   0.102  0.91900    
## ViralLoad:Treatmentd4t+ddI  0.439794   0.308829   1.424  0.15443    
## ViralLoad:Treatmentswitch   0.008679   0.291172   0.030  0.97622    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Correlation of Fixed Effects:
##             (Intr) VirlLd Trt4+I Trtmnt VL:T4+
## ViralLoad   -0.780                            
## Trtmntd4t+I -0.616  0.473                     
## Trtmntswtch -0.679  0.521  0.423              
## VrlLd:Tr4+I  0.518 -0.657 -0.821 -0.355       
## VrlLd:Trtmn  0.549 -0.695 -0.341 -0.786  0.475

  1. Jean-Michel Molina et al. “The ALBI Trial: A Randomized Controlled Trial Comparing Stavudine Plus Didanosine with Zidovudine Plus Lamivudine and a Regimen Alternating Both Combinations in Previously Untreated Patients Infected with Human Immunodeficiency Virus,” The Journal of Infectious Diseases 180, no. 2 (1999): 351–358, doi:10.1086/314891.↩︎

Last updated on October 31, 2025

Edit this page